|
НАУКА
Новости
Научный форум

Космические новости
Энциклопедия космонавтика
Энциклопедия "Естествознание"
Журнальный зал
Физматлит
News of Russian Science and Technology
Научные семинары
Почему молчит Вселенная?
Парниковая катастрофа
Кто перым провел клонирование?
Хронология и парахронология
История и астрономия
Альмагест
Наука и культура
Журналы в сети:
Nature
Успехи физических наук
New Scientist
ScienceDaily
Discovery
ОБРАЗОВАНИЕ
Открытое письмо министру образования
Антиреформа
Соросовский образовательный журнал
Биология
Науки о Земле
Математика и Механика
Технология
Физика
Химия
Русская литература

КОНКУРСЫ

Для молодых биологов
БИБЛИОТЕКИ
Библиотека Хроноса
Научпоп
РАДИО
Читают и поют авторы РП
ОТДЫХ
Музеи
Игры
Песни русского застолья
Народное
Смешное
О НАС
Редколлегия
Авторам
О журнале
Как читать журнал
Пишут о нас
РЕСУРСЫ
Поиск
Проекты
Посещаемость
Журналы
Русские писатели и поэты
Избранное
Библиотеки
Фотоархив
ИНТЕРНЕТ
Топ-лист "Русского переплета"
Баннерная сеть
Наши баннеры
НОВОСТИ
Все
Новости русской культуры
Новости науки
Космические новости
Афиша
The best of Russian Science and Technology
|
"Русский переплет" зарегистрирован как СМИ.
Свидетельство о регистрации в Министерстве печати РФ: Эл. #77-4362 от
5 февраля 2001 года. При полном или частичном использовании
материалов ссылка на www.pereplet.ru обязательна.
|
<< 11|12|13|14|15|16|17|18|19|20 >> ... Все
|
14.02.2015
00:41 |
Русские открыли - европейцы сделали
Европейская Южная обсерватория, 3.6-м телескоп NTT(The ESO New Technology Telescope) на горе La Silla(Chile) получил спектр для Сверхновой, открытой на телескопе МАСТЕР-Тунка с помощью . . . |
|
05.02.2015
23:52 |
Новая экзопланета типа Земли и Великое Молчание Вселенной
В апреле 2014 года при помощи телескопа НАСА Kepler была открыта экзопланета, получившая название Кеплер-186F. Планета расположена на расстоянии в 490 световых лет от . . . |
|
02.02.2015
16:33 |
Глобальная сеть МАСТЕР не пропустила проход потенциально-опасного астероида 2004BA86 12 мимо Земли (Видео).
Видео съёмки астероида 2004BA86 12 пролетавшего 26 января мимо Земли пунктом Глобальной Роботизированной сети МАСТЕР, расположенном на базе Московского и Иркутского . . . |
|
31.01.2015
01:53 |
Компания MercatorInfogr сделала ролик о МАСТЕРе
Появился ролик про нашу сеть МАСТЕР. Приятно, что люди по своей инициативе потратили время на популяризацию достижений отечественной науки. За исключением . . . |
|
19.01.2015
20:04 |
МАСТЕР открыл яркую вспышку Новой звезды в галактике Андромеда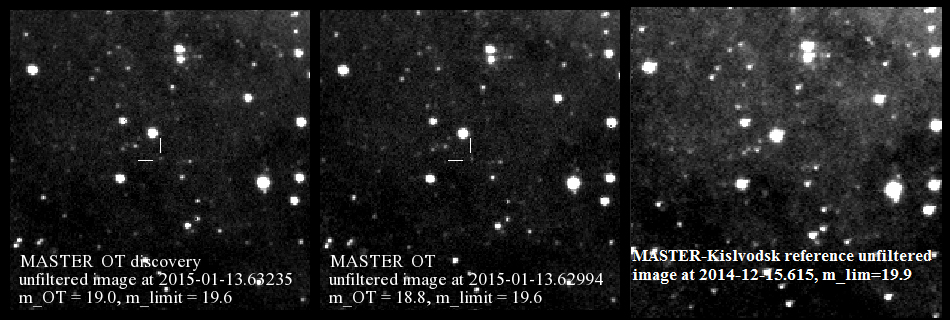
Далекий взрыв, зафиксированный российским роботом-телескопом МАСТЕР случился два с половиной миллиона лет назад, когда еще не появился на Земле вид Homo Sapiens . . . |
|
15.01.2015
17:46 |
Байкальский МАСТЕР снял комету C/2014 Q2 (Лавджоя) 
Маша Пружинская и Наташа Тюрина сняли комету C/2014 Q2 (Лавджоя) с помощью телескопа-робота МАСТЕР расположенного вблизи Байкала (вишь, не только русская женщина коня . . . |
|
08.01.2015
13:34 |
Эта странная конструкция является символом возрождения России
Виктор Сеник с Кавказских гор шлёт закат над Кисловодским МАСТЕРом и поздравления c Рождеством! Друзья, эта странная конструкция является символом возрождения . . . |
|
02.01.2015
21:52 |
МАСТЕР признан лучшим научным проектом года
По мнению издания Электронные Бюллетень" (Декабрь 2014, N51) Значимость сети «МAСТЕР» (как программную составляющую, так и телескопическую) уже давно оценила мировая . . . |
|
30.12.2014
19:11 |
Как строился МАСТЕР в Южной Африке. Видео.  " "
Здесь вы найдете процесс установки российского робота-телескопа МАСТЕР IIm в обсерватории Сазерленд (Южная Африка). Собственно фильм начинается 4 декабря, когда . . . |
|
29.12.2014
19:23 |
Презентация телескопа МАСТЕР-SAAO, установленного в Южной Африке. Видео.
Смотрите репортаж об открытии российско-южно-африканского телескопа: . . . |
|
24.12.2014
13:30 |
Пресс-конференция об открытии русско-южно-африканского проета МАСТЕР-SAAO
Дорогие друзья! Надеюсь, к Новому Году российским читателям, зрителям и слушателям интересно будет узнать, что в Южной Африке, в Астрономической обсерватории . . . |
|
22.12.2014
20:40 |
Русский телескоп-робот МАСТЕР заработал в Южной Африке!
Этот научный отчет посвящаю Жене Горбовскому, который и получил первый свет в Южной Африке, как подарок своему сыну Ярославу, рожденному сегодня! Ура!!! С 1-го . . . |
|
25.11.2014
13:48 |
Новость
|
|
14.11.2014
16:29 |
Здравствуй, племя молодое - незнакомое или как объяснить на пальцах решение Лифшица!
Ваш покорный слуга недавно выиграл грант фонда "Династия", по которому мне довелось снова побывать на своей Родине - Дальнем Востоке - и прочитать курс лекций "Космология и физика элементарных частиц". Хочу похвастаться, что мне удалось объяснить будущим учителям, а, возможно, и ученым, зачем нужны тёмная энергия, тёмная материя и почему нужна модель инфляции, не прибегая к дифференциальным уравнениям! Бьюсь об заклад - этого не смог бы сделать даже Стивен Хоукинг, написавший не одну книгу-бестселлер по космологии для домохозяек!
Замечательные студенты (и студентки) приходили ко мне на лекции. Выдержать 2 пары в день по космологии - это что-то да значит! (См. Вверху фото. Благовещенский
Педагогический Государственный университет, 14 ноября, 2014 г.)
Причем я их не баловал презентациями в стиле непрерывного показа голливудских картинок с космического телескопа Хаббл, а читал в духе принципа - "книга лучше кино" и пользовался только доской и мелом. Самое сложное - это было объяснить на пальцах формулу роста возмущений в расширяющейся Вселенной, впервые открытую Евгением Лифшицем (многолетним соавтором Ландау), который получил ее путем решения уравнений Эйнштейна методом возмущений. Здесь мне помогла старая идея моего учителя Якова Борисовича Зельдовича, который как-то на лекции по космологии обронил, что мол, можно не решая дифференциальные уравнения, получить знаменитое решение Лифшица для задачи Джинса в расширяющейся Вселенной. Я уже давно научился так получать падающую "моду" (это слово в данном контексте не имеет отношения к шоу-бизнесу), согласно которой относительные возмущения плотности растут обратно пропорционально времени:
(Delta ro)/ro ~ T-1,
где T - время, а ro - невозмущенная плотность Вселенной.
Это элементарно получается, если рассмотреть расширение маленького шара в однородной Вселенной, "задержавшегося в своем развитии", то есть шара, который начал немного позже расширяться, чем вся остальная Вселенная. Смотрите за руками:
Плотность в однородной, расширяющейся с критической плотностью Вселенной (со второй космической скоростью) меняется по закону:
ro ~ 1/T2
Теперь запишем такую же формулу для шарика, задержавшегося в своем развитии на время delta T:
ro ~ 1/(T + delta T)2
Вычитая одну формулу из другой, а затем разделив результат на плотность невозмущенной Вселенной, находим первое решение Лифшица. Но оно не очень интересное, потому что падает со временем и, следовательно, не приводит к гравитационной неустойчивости, то есть к образованию объектов во Вселенной.
Но есть вторая - растущая "мода" - согласно которой возмущения плотности растут, и именно благодаря ей во Вселенной образовались скопления галактик, сами галактики, звезды, планеты и, наконец, мы с вами.
(Delta ro)/ro ~ T2/3
Я неоднократно пытался получить это решение предыдущим методом, но никак не получалось. И наконец я вспомнил о своей любимой книге, которую когда-то давно (в 1974 году) включил в "Студенческий ужин": 
В.М.Липунов. Натюрморт "Студенческий ужин". Картон/Масло. 1974. В центре - книга Я.Б.Зельдовича и И.Д.Новикова "Релятивистская астрофизика". Подобно Дюрреру, который изобразил Иоанна Богослова, поедающего Библию, я попытался изобразить ужин студента, поедающего хлеб, лук с солью и книгу "Релятивистcкая астрофизика".
Эта замечательная книга, наполненная искрящимися идеями, содержит то самое решение на пальцах, о котором говорил Зельдович на лекциях.
Чтобы его получить, нужно снова рассмотреть возмущенный шарик, но не запоздавший "стартануть", а шарик, имеющий скорость немного меньше второй космической! Поклон ЯБ, столетие которого мы отмечаем в текущем году.
Пока я читал свои лекции, налетели сибирские ветры и наступила настоящая зима.

Берег Амура. Благовещенск. 13 ноября 2014 г. Приморозило сегодня с ветерком. Но... Амур плавно несёт воды свои, и сибирские ветры песни ему поют. Город прекрасен. Набережные одеваются в бетон, а торпедные катера стоят на постаментах.
Звучит (в душе) музыка в исполнении Ансамбля Советской Армии...

 �
�
|
|
30.10.2014
13:00 |
Русский МАСТЕР открыл новый опасный астероид, который угрожает Венере, Марсу и Земле и размером превосходит Апофиз
Единственая в России сеть роботов-телескопов МАСТЕР созданная МГУ им.М.В.Ломоносова в содружестве с 3-мя отечественными университетами (Екатеринбурга, Иркутска, . . . |
|
29.10.2014
16:56 |
Русский МАСТЕР заставил повернуться крупнейшие 8-метровые телескопы Европейской Обсерватории в Чили и Gemini на Гаваях
Речь опять идет о гамма-всплесках - самых мощных взрывах во Вселенной, о процессах как мы думаем в которых образуются керровские черные дыры. Недавно мы писали как . . . |
|
25.10.2014
17:29 |
Кто украл красный гигант или как российский робот МАСТЕР обнаружил самую догопериодическую затменную двойную?
Денис Денисенко сообщает: "Неожиданное продолжение получила история с открытием первого оптического анти-транзиента МАСТЕРа (потухшей звезды в созвездии Малого . . . |
|
19.09.2014
11:16 |
Русский МАСТЕР нашел потерянный американцами опасный астероид
Последние несколько дней весь коллектив лаборатории космического мониторинга занимался написанием грантов. Дело это времени затратное, вредное и часто . . . |
|
03.08.2014
19:19 |
1 августа 2014 года наш робот-МАСТЕР заставил повернуться самый большой в мире телескоп.
1 августа 2014 года наш робот-МАСТЕР заставил повернуться самый большой в мире телескоп. За ним поехали и миллиардный СВИФТ с другими помельче. Конечно мы и раньше . . . |
|
24.04.2014
20:39 |
МАСТЕР открыл самый мощный стационарный объект во Вселенной
Денис Денисенко сообщает: Астрономы Российской Глобальной сети телескопов-роботов МАСТЕР Московского государственного университета, обнаружили ярчайшую . . . |
<< 11|12|13|14|15|16|17|18|19|20 >> ... Все
|
ЛИТЕРАТУРА
Новости русской культуры
К читателю
Содержание
Публицистика
"Курск"
Кавказ
Балканы
Проза
Поэзия
Драматургия
Искания и размышления
Критика
Сомнения и споры
Новые книги
У нас в гостях
Издательство
Книжная лавка
Журнальный зал
ОБОЗРЕНИЯ
"Классики и современники"
"Слово о..."
"Тайная история творений"
"Книга писем"
"Кошачий ящик"
"Золотые прииски"
"Сердитые стрелы"
КУЛЬТУРА
Афиша
Новые передвжиники
Фотогалерея
Музыка
"Неизвестные" музеи
Риторика
Русские храмы и монастыри
Видеоархив
ФИЛОСОФИЯ
Современная русская мысль
Искания и размышления
ИСТОРИЯ
ХРОНОС
История России
История в МГУ
Слово о полку Игореве
Хронология и парахронология
Астрономия и Хронология
Альмагест
Запечатленная Россия
Сталиниана
ФОРУМЫ
Дискуссионный клуб
Научный форум
Форум "Русская идея"
Форум "Курск"
Исторический форум
Детский форум
КЛУБЫ
Пятничные вечера
Клуб любителей творчества Достоевского
Клуб любителей творчества Гайто Газданова
Энциклопедия Андрея Платонова
Мастерская перевода
КОНКУРСЫ
За вклад в русскую культуру публикациями в Интернете
Литературный конкурс
Читательский конкурс
Илья-Премия
ДЕТЯМ
Электронные пампасы
Фантастика
Форум
АРХИВ
2001
2000
1999
Фотоархив
Все фотоматериалы
|













 "
" 






 �
�




